Implementing transitive closure in arithmetic
Let T(x,y) be an arithmetical formula with two free variables x and y.
Its reflexive and transitive closure T*(x,y) is the smallest
predicate satisfying
- T*(x,x),
- if T(x,y) then T*(x,y),
- and if T*(x,y) and T*(y,z) then T*(x,z).
Equivalently, T*(x,y) holds if and only if their exists a nonempty
finite sequence of natural numbers an ... a2
a1 a0 such that x = an, y = a0
and for i = 0,...,n-1 one has T(ai,ai+1).
In this note I will show how to implement T*(x,y) in the language of
arithmetic.
Any nonempty finite sequence of natural numbers an ...
a2 a1 a0 can be encoded as a single number t,
namely by selecting a number p that is larger than all of them and
regarding an...a2a1a0
to be the p-ary representation of t. The sequence 3 5 7 0 1 for
instance could be encoded by the number 35701, if one selects p to be 10.
The number t is calculated by the formula t = 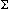 i=0n ai pi.
The sequence 3 5 13 0 1 can not be encoded in base 10 however.
For this sequence one needs to choose p larger than 13. In general the
choice of p depends on the sequence, so the sequence is encoded not
just by t, but really by the pair (t,p).
i=0n ai pi.
The sequence 3 5 13 0 1 can not be encoded in base 10 however.
For this sequence one needs to choose p larger than 13. In general the
choice of p depends on the sequence, so the sequence is encoded not
just by t, but really by the pair (t,p).
This encoding is not unique however. The pair (35701,10) for instance
is the encoding of the sequence 3 5 7 0 1, but it is also the encoding
of the sequence 0 3 5 7 0 1. Because uniqueness is important here, I
choose (35701,10) to be the encoding of the sequence 3 5 7 0 1 only,
i.e. I only encode sequences an ...
a2 a1 a0 with an > 0.
Now a pair (0,p) does not encode a sequence, but any pair (t,p) with t
> 0 does.
Write Last(t,p,y) if y is the last number in the sequence encoded by t
and p, i.e. if y = a0. The formula Last(t,p,y) can be
expressed arithmetically as
y < p 
 r (t = rp+y).
r (t = rp+y).
Write First(t,p,x) if x is the first number in the sequence encoded by
t and p, i.e. if x = an. The formula First(t,p,x) can be
expressed arithmetically as
0 < x < p 
 n
n  s
(t = xpn+s
s
(t = xpn+s  s < pn).
s < pn).
Write Neighbours(t,p,u,v) if u and v are neighbours in the sequence
encoded by t and p, i.e. if there is an i < n such that u = ai+1
and v = ai. The formula Neighbours(t,p,u,v) can be
expressed arithmetically as
u < p  v < p
v < p 
 i
i
 r
r
 s
(t = rpi+2+upi+1+vpi+s
s
(t = rpi+2+upi+1+vpi+s
 s < pi
s < pi
 r+u > 0).
r+u > 0).
Here the condition u+r > 0 says that either u or r is positive, which
is the case exactly when i < n. I couldn't write i < n directly, as
the value of n varies with the sequence.
Now the reflexive and transitive closure T*(x,y) of a formula T(x,y)
with free variables x and y can almost be defined by
 t
t
 p
(First(t,p,x)
p
(First(t,p,x)  Last(t,p,y)
Last(t,p,y)
 (Neighbours(t,p,u,v)
(Neighbours(t,p,u,v)
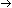 T(u,v)).
T(u,v)).
This formula says that there is a sequence an ...
a2 a1 a0 of numbers, such that the
first one (an) is x, the last one is y, and whenever u and
v are neighbours in the sequence, then T(u,v). There is however one
mistake in this formula, namely it insists that x > 0. This problem
can be solved by encoding the sequence an+1 ...
a2+1 a1+1 a0+1 as a pair (t,p).
Doing so doesn't require an to be positive, as an+1
is always positive. A correct definition of T*(x,y) therefore is
 t
t
 p
(First(t,p,x+1)
p
(First(t,p,x+1)  Last(t,p,y+1)
Last(t,p,y+1)
 (Neighbours(t,p,u+1,v+1)
(Neighbours(t,p,u+1,v+1)
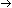 T(u,v)).
T(u,v)).
The construction above generalizes easily from relations between
numbers to relations between vectors of numbers. I will illustrate
this for vectors of length 3, but the number 3 plays no special role
here. The case of length 3 is what I need in
my proof of Goedel's incompleteness theorem.
Let T(x1,x2,x3,y1,y2,y3)
be an arithmetical formula with six free variables x1,
x2, x3, y1, y2 and y3.
Its reflexive and transitive closure
T*(x1,x2,x3,y1,y2,y3)
is the smallest predicate satisfying
- T*(x1,x2,x3,x1,x2,x3),
- if T(x1,x2,x3,y1,y2,y3) then T*(x1,x2,x3,y1,y2,y3),
- and if
T*(x1,x2,x3,y1,y2,y3)
and
T*(y1,y2,y3,z1,z2,z3)
then
T*(x1,x2,x3,z1,z2,z3).
Equivalently,
T*(x1,x2,x3,y1,y2,y3)
holds if and only if their exists three equally long nonempty
finite sequences of natural numbers an ... a2
a1 a0 and bn ... b2
b1 b0 and cn ... c2
c1 c0 such that x1 = an,
x2 = bn, x3 = cn,
y1 = a0, y2 = b0,
y3 = c0
and for i = 0,...,n-1 one has T(ai,bi,ci,ai+1,bi+1,ci+1).
Next I will show how to implement T*(x1,x2,x3,y1,y2,y3) in the language of arithmetic.
Three equally long nonempty finite sequences of natural numbers
an ... a2 a1 a0 and
bn ... b2 b1 b0 and
cn ... c2 c1 c0
can be encoded by three numbers t1, t2 and
t3, namely by selecting a number p that is larger than all
numbers in the three sequences and
regarding an...a2a1a0
to be the p-ary representation of t1, and
bn...b2b1b0
to be the p-ary representation of t2, and
cn...c2c1c0
to be the p-ary representation of t3.
The triple of sequences is thus encoded by the quadruple
(t1,t2,t3,p).
In order to make the encoding unique, I only encode sequences in which
an > 0 and bn > 0 and cn > 0.
Write Last(t1,t2,t3,p,y1,y2,y3) if
y1, y2 and y3 are the last numbers in
the sequences, i.e. if (y1,y2,y3) =
(a0,b0,c0). The formula
Last(t1,t2,t3,p,y1,y2,y3) can be expressed
arithmetically as
y1 < p 
 r1 (t1=r1p+y1)
r1 (t1=r1p+y1)
 y2 < p
y2 < p 
 r2 (t2 = r2p+y2)
r2 (t2 = r2p+y2)
 y3 < p
y3 < p 
 r3 (t3 = r3p+y3).
r3 (t3 = r3p+y3).
Write First(t1,t2,t3,p,x1,x2,x3) if
x1, x2 and x3 are the first numbers in
the sequences, i.e. if (x1,x2,x3) =
(an,bn,cn). The formula
First(t1,t2,t3,p,x1,x2,x3) can be expressed
arithmetically as
0 < x1 < p  0 < x2 < p
0 < x2 < p  0 < x3 < p
0 < x3 < p 
 n (
n (
 s1
(t1 = x1pn+s1
s1
(t1 = x1pn+s1
 s1 < pn)
s1 < pn)

 s2
(t2 = x2pn+s2
s2
(t2 = x2pn+s2
 s2 < pn)
s2 < pn)

 s3
(t3 = x3pn+s3
s3
(t3 = x3pn+s3
 s3 < pn)
).
s3 < pn)
).
Write Neighbours(t1,t2,t3,p,u1,u2,u3,v1,v2,v3)
if (u1,u2,u3) and
(v1,v2,v3) are neighbours, i.e. if
there is an i < n such that u1 = ai+1 and
u2 = bi+1 and u3 = ci+1
and v1 = ai and v2 = bi
and v3 = ai. The formula
Neighbours(t1,t2,t3,p,u1,u2,u3,v1,v2,v3)
can be expressed arithmetically as
u1 < p  u2 < p
u2 < p  u3 < p
u3 < p  v1 < p
v1 < p  v2 < p
v2 < p  v3 < p
v3 < p 
 i (
i (
 r1
r1
 s1
(t1=r1pi+2+u1pi+1+v1pi+s1
s1
(t1=r1pi+2+u1pi+1+v1pi+s1
 s1 < pi
s1 < pi
 r1+u1 > 0)
r1+u1 > 0)

 r2
r2
 s2
(t2 = r2pi+2+u2pi+1+v2pi+s2
s2
(t2 = r2pi+2+u2pi+1+v2pi+s2
 s2 < pi
s2 < pi
 r2+u2 > 0)
r2+u2 > 0)

 r3
r3
 s3
(t3 = r3pi+2+u3pi+1+v3pi+s3
s3
(t3 = r3pi+2+u3pi+1+v3pi+s3
 s3 < pi
s3 < pi
 r3+u3 > 0)
).
r3+u3 > 0)
).
Now the reflexive and transitive closure
T*(x1,x2,x3,y1,y2,y3)
of a formula
T(x1,x2,x3,y1,y2,y3)
with free variables x1,
x2, x3, y1, y2 and
y3 can be defined by
 t1
t1
 t2
t2
 t3
t3
 p
(First(t1,t2,t3,p,x1+1,x2+1,x3+1)
p
(First(t1,t2,t3,p,x1+1,x2+1,x3+1)  Last(t1,t2,t3,p,y1+1,y2+1,y3+1)
Last(t1,t2,t3,p,y1+1,y2+1,y3+1)
 (Neighbours(t1,t2,t3,p,u1+1,u2+1,u3+1,v1+1,v2+1,v3+1)
(Neighbours(t1,t2,t3,p,u1+1,u2+1,u3+1,v1+1,v2+1,v3+1)
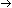 T(u1,u2,u3,v1,v2,v3)).
T(u1,u2,u3,v1,v2,v3)).
If arithmetic would be defined so as to contain exponentiation, the
above implementation would be complete (considering that a < b can be
rewritten as  k: a+1+k = b).
k: a+1+k = b).
However, arithmetic only features 0,1,+,x and =. The reason that
exponentiation is not included in the definition of arithmetic, is that
it doesn't add to the expressiveness of the language: the formula
x = yn is expressible in exponentiation-free arithmetic:
Let E(i,u,y,j,v,y') be the formula
i = j+1  u = vy
u = vy  y' = y
y' = y
then x = yn holds iff E*(n,x,y,0,1,y), where E* is the
reflexive and transitive closure of E.
As this implementation of exponentiation involves the reflexive and
transitive closure, is it necessary to express reflexive and
transitive closure in exponentiation-free arithmetic. This is done as
follows. The statement
"p is prime" 
 n (q = pn)
n (q = pn)
can be implemented in arithmetic as
 d (
d
d (
d  1
1 
 k (q = kd)
k (q = kd)
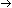
 k (d = kp)
)
k (d = kp)
)
which says that for any divisor d of q with d  1, p must be a divisor of d. This implies that p is a prime
divisor of q and q has no other prime divisors than p.
1, p must be a divisor of d. This implies that p is a prime
divisor of q and q has no other prime divisors than p.
The only requirement on the number p in the implementation of
reflexive and transitive closure above, is that it is sufficiently large.
No generality is lost if one requires p to be prime.
Now the formula First(t,p,x) can be reformulated as
0 < x < p 
 q
("p is prime"
q
("p is prime" 
 n (q = pn)
n (q = pn)

 s
(t = xq+s
s
(t = xq+s  s < q)).
s < q)).
Likewise Neighbours(t,p,u,v) can be reformulated as
u < p  v < p
v < p 
 q
("p is prime"
q
("p is prime" 
 i (q = pi)
i (q = pi)

 r
r
 s
(t = rqpp+uqp+vq+s
s
(t = rqpp+uqp+vq+s
 s < q
s < q
 r+u > 0)).
r+u > 0)).
In these formulas the use of exponentiation can be eliminated as
indicated above. The same holds for the generalization to relations
between vectors of numbers (of length 3 or otherwise).
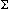 i=0n ai pi.
The sequence 3 5 13 0 1 can not be encoded in base 10 however.
For this sequence one needs to choose p larger than 13. In general the
choice of p depends on the sequence, so the sequence is encoded not
just by t, but really by the pair (t,p).
i=0n ai pi.
The sequence 3 5 13 0 1 can not be encoded in base 10 however.
For this sequence one needs to choose p larger than 13. In general the
choice of p depends on the sequence, so the sequence is encoded not
just by t, but really by the pair (t,p).

 r (t = rp+y).
r (t = rp+y).
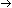 T(u,v)).
T(u,v)).
 d (
d
d (
d  1
1