 Course notes for CS154
Course notes for CS154
This file will keep track of the material covered so far, and list the
handouts distributed to date.
Preliminaries
Chapter 0.1 of the book tells you where this course will be about.
Read it before taking this class, together with the first section of
the preface. The rest of Chapter 0 consist of preliminaries that you
should have encountered in CS103 or other courses. Please leaf through
this chapter to check that you are acquainted with its contents. Ask
us for help if necessary, preferably prior to the first class. During
the first lecture, homework will be assigned on
this material.
Wednesday, April 3
I presented an overview of the course, also treating this handout. Then I made a start
with the first of the four subjects of this course, namely regular
languages. I introduced DFAs, NFAa and regular expressions and told
how they define languages. Next week I will show that these three
methods are equally powerful, i.e. define the same class of languages,
the regular ones. In terms of Sipser, I treated Section 1.1 until
page 44, Section 1.2 until page 54 and 1.3 until page 66.
It helps if you reread the same material from the book.
Homework is on the web.
Monday, April 8
Today I showed the equivalence of the three approaches to defining
regular languages. I also showed that regular languages are closed
under intersection (besides being closed under the regular operators).
This finishes Section 1.3 of Sipser, and everything before that.
For the readers of Hopcroft & Ullman (HU): We have covered Chapters 1
and 2 now, while skipping 2.6 - 2.8. (The applications in Section 2.8
may be good to read though.) Wednesday Chapter 3.
For the readers of Hopcroft, Motwani & Ullman (HMU): We have covered
Chapters 1, 2 and 3, while skipping Sections 2.4, 3.3 and 3.4. (The
applications in Sections 2.4 and 3.3 may be good to read though.)
Wednesday Chapter 4.
Wednesday, April 10
Today I presented two tools for proving languages not to be regular:
the pumping lemma, and closure properties. Subsequently
I showed how to make sure that a DFA has as few states as possible, by
calculating which states are equivalent and identifying
equivalent states. This subject (minimization) is covered in HMU, but
not in Sipser. Therefore I hereby present this handout. Finally I showed
how three basic problems that are unsolvable in some other classes of
languages, can be solved for regular languages, namely the question
whether a given string belongs to a given regular language, whether a
regular language is empty, and whether two regular languages are
equal. In all the cases the regular languages may be given as DFAs,
NFAs or regular expressions.
Covered material on regular languages: Sipser Chapter 1 (all of
it) and minimization of DFAs
(not in Sipser). Also the easy algorithms below.
This corresponds to HMU Chapter 2 (except 2.4), 3 (except 3.3-4), and
4 (except 4.2.3-4),
and to HU Chapter 2 (except 2.7-8) and 3 (except Theorems 3.9-10).
Important topics:
- DFAs and NFAs recognize, and regular expressions generate, the same
class of languages, called the regular languages.
- These languages are closed under intersection, union,
concatenation, star, complement and reversal.
- The pumping lemma and the closure properties are the main tools
for showing languages to be non-regular.
- There are easy algorithms for
Friday, April 12
Aaron gave the first discussion session today. Here are his notes:
page 1,
page 2 &
page 3.
Monday, April 15
I presented context-free languages by means of context-free grammars
as well as pushdown automata. Wednesday I will show that these methods
are equally powerful. I showed that regular languages are context-free.
I also treated parsing, ambiguity, and "repairing" ambiguous grammars.
Wednesday, April 17
Today I showed that any CFG can be converted into a PDA accepting the
same language, and, vice versa, any PDA can be converted into a CFG
generating the same language. I also explained that PDAs that accept
by empty stack are equally powerful as PDAs accepting by final state.
Deterministic CFLs are languages accepted, by final state, by
deterministic pushdown automata. These are pushdown automata that in
any state, for any possible input and stack content, can do at most
follow one possible transition. For deterministic PDAs acceptance by
empty stack would not be powerful enough. The regular languages are
seen to be a subclass of the deterministic context-free languages,
which are a subclass of the context-free languages.
I also showed how any CFG can be converted into Chomsky normal form.
This yields an algorithm to decide whether a given string is generated
by a given context-free grammar. And I introduced the concept of an
inherently ambiguous context-free language.
Friday, April 19
Arun gave the second discussion session today.
Here is his handout..
Aaron produced a handout that shows a conversion from a PDA to a CFG,
available as dvi,
ps and pdf.
Monday, April 22
I finished the treatment of context-free languages by explaining the
pumping lemma, closure properties, and some easy algorithms and the
absence thereof (see below, and compare with the ones for regular languages).
Covered material on context-free languages: Sipser Chapter 2 (all of
it) and the concept of useless variables
(not in Sipser). Also the easy algorithms below.
Furthermore deterministic pushdown automata, and the notion of
acceptance by empty stack.
This corresponds to HMU Chapters 5, 6 and 7, except Sections 5.3, 6.4.4,
7.3.1, 7.3.2, 7.3.5 and 7.4 (but the very beginning of 7.4.4 and
7.4.5. is treated),
and to HU Chapters 4, 5 and 6, except Sections 4.6-7,
Theorems 6.2-3 and the end of Section 6.3.
Important topics:
- Context-free grammars generate, and pushdown automata recognize, the
same class of languages, called the context-free languages.
- These languages are closed under union, concatenation, star and
reversal, as well as intersection with a regular language.
They are not closed under complementation and intersection.
- The pumping lemma and the closure properties are the main tools
for showing languages to be non-regular.
- Parsing, ambiguity, inherently ambiguous languages.
- There are easy algorithms for
On the other hand, there are no algorithms whatsoever for
- checking whether two CFGs generate the same language,
- checking whether a given CFG is ambiguous,
- checking whether the intersection of two context-free
languages (given by CFGs or PDAs) is empty,
- and checking whether the language accepted by a given
pushdown automaton or CFG consists of all strings over the given
alphabet (i.e. whether its complement is empty).
The midterm exam covers all the material on
regular and context-free languages mentioned above.
 CS154N
CS154N
This part of the course deals with Parts Two and Three of the book.
Wednesday, April 24
I started off by introducing the concept of decidability
without using Turing machines and Church's thesis, following
this handout.
Please read the handout carefully before the next lecture.
Friday, April 26
Elena gave the third discussion session today.
Here are her notes.
Monday, April 29
I presented Turing machines, and their connection (through Church's
thesis) with decidability. By the Church-Turing thesis a language L is
recursive enumerable (called Turing-recognizable in
Sipser) if and only if it is semi-decidable (or
recognizable, or enumerable). In other words: if there
is any algorithm that when given a string w as input accepts
exactly when w is in L, then there is a Turing machine with
that property. Likewise, a language L is recursive if and only
if it is decidable. In other words: if there is any algorithm
that when given a string w as input accepts exactly when
w is in L and rejects otherwise, then there is a Turing machine
with that property. Church's thesis is not a mathematical theorem, but
a reflection on the inability of computer scientists since 1936 to
come up with any algorithm whatsoever that cannot be translated into a
Turing machine.
I showed that one-tape Turing machines are equivalent to multitape
Turing machines, and mentioned that there are many variations of
Turing machines of this nature.
Wednesday, May 2
I showed that nondeterministic Turing machines are equally expressive
as deterministic ones. Thereby Chapter 3 of Sipser is covered entirely.
I also introduced Grammars, which
are generalizations of context-free grammars, not covered in Sipser.
A language is generated by a grammar if and only if it is recursive
enumerable.
| Regular languages | Context-free languages | Context
sensitive languages | Recursive enumerable languages |
Chomsky hierarchy
| Regular expressions | Context-free grammars |
Context sensitive grammars | unrestricted grammars |
| NFA | PDA | LBA | nondeterministic Turing
machines |
| DFA | (DPDA are weaker) | (DLBA are weaker) |
Turing machines |
I completed the treatment of the Chomsky hierarchy (depicted above,
and originally proposed as four candidates for modeling natural
languages) by defining the context sensitive languages. These
are generated by context sensitive grammars, and can be
recognized by nondeterministic Turing machines that use no more space
than the length of the input string. Such machines are called
Linear Bounded Automata.
I presented the concept of an enumerator and showed that a language is
enumerable if and only if it is semi-decidable (see last week's
handout).
I defined the notion of cardinality and showed that there
are equally many rational numbers (fractions) as natural numbers
(non-negative integers): the rational numbers are countable.
However, there are more real numbers than natural numbers: the reals
are uncountable. This I showed with the method of diagonalization.
The same method also yields that there are countably many algorithms,
but uncountably many languages. Thus there must be languages whose
membership cannot be semi-decided by means of any algorithm.
In fact one such language was constructed last week already, in the
handout on decidability.
I touched upon the notion of reducing one problem to another, and used
it to prove that the acceptance problem is undecidable. In terms of
general algorithms this is treated in my
decidability handout; in terms
of Turing machines in the textbooks. Chapter 4 of Sipser is now
considered completely covered, as well as the very beginning of
Chapter 5.
Thursday, May 3
In view of the midterm exam on Friday afternoon, there will be no
discussion session on Friday morning. Instead, there will be a midterm
review session on Thursday morning, presented by Aaron, from 9:30 to
10:20am in McCullough 115, live on channel E1.
Monday, May 6
Fix a suitable alphabet 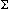 ,
and consider languages over
,
and consider languages over 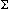 .
The acceptance problem for Turing machines, APTM is
the language
.
The acceptance problem for Turing machines, APTM is
the language
APTM = { (<M>,w) |
Turning machine M accepts input string w}
where <M> denotes the description of M as a string over
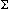 .
Because this is such an important issue I once more reviewed the
undecidability of APTM.
The language
.
Because this is such an important issue I once more reviewed the
undecidability of APTM.
The language
SELF-REJECTTM = { <M> |
Turning machine M does not accept input string <M>}
can be seen to be not Turing-recognizable by means of a direct
paradoxical contradiction, or by means of a diagonalization argument.
Hence the language
SELF-ACCEPTTM = { <M> |
Turning machine M accepts input string <M>}
must be undecidable, using closure of decidability under
complementation and intersection, and Church's thesis.
Now APTM is undecidable because the language
SELF-ACCEPTTM can be reduced to APTM,
by substituting <M> for w.
It is important to apply reductions in the right direction (see above)!
I showed that it is undecidable whether a given Turing machine accepts
the empty language, by reducing the acceptance problem (which is known
to be undecidable) to it. This is a special case of Rice's theorem,
which says that any nontrivial property about the language recognized
by a Turing machine is undecidable. I proves Rice's theorem, which
is not covered in Sipser, using this
handout.
Wednesday, May 8
Today I proved the undecidability of the emptiness problem for
linear bounded automata, and of the Post correspondence problem.
I didn't finish the latter, but you should read the rest of it in the
book.
Friday, May 10
Aaron gave today's section. Here are his notes:
page 1,
page 2,
page 3,
page 4,
page 5 &
page 6.
Or smaller versions if they don't fit your screen:
page 1,
page 2,
page 3,
page 4,
page 5 &
page 6.
Monday, May 13
I finished the treatment of the Post Correspondence Problem.
Then I introduced computable (or
recursive) and partial recursive functions and explained the difference
between mapping reducibility and Turing reducibility.
Subsequently I'll treated the undecidability
of the empty intersection problem for context-free grammars (not
covered in Sipser). Consult this handout for the undecidability of
the ambiguity problem for CFGs.
During this course I plan to cover also a few more advanced topics in
computability (or decidability) theory; however, these will be
postponed until after the treatment of complexity theory.
This because it is very important that you get the homeworks on
complexity theory back well before the final exam.
Covered material on computability theory:
Sipser Chapters 3, 4, 5 (except for the proof of theorem 5.10 (but the
statement is covered)), and 6.3, as well as the handouts linked below.
This corresponds to HMU Chapters 8 and 9, except Sections 8.5.3, 8.5.4
and 9.5.3, plus the handouts.
Important topics:
- Decidable, recognizable and
enumerable languages; recursive, Turing-recognizable and recursive
enumerable languages; the relationships between these classes;
Church's thesis.
- The decidable languages are closed under union, intersection and
complementation; r.e. languages under union and intersection, but not
complementation.
- The existence of unrecognizable languages, and of recognizable
but undecidable languages.
- Diagonalization. Countability.
- Turing machines; configurations; multitape TMs; the equivalence
of deterministic and nondeterministic TMs.
- Unrestricted and Context-sensitive
grammars. Linear Bounded Automata .
- Computable (or recursive) and
partial recursive functions.
- The method of reduction. Mapping reducibility and Turing reducibility.
- Undecidability of the acceptance problem for TMs, the halting
problem, whether an algorithm halts on all inputs, the emptiness
problem for TMs, the emptiness problem for LBAs, Post Correspondence
Problem, ambiguity of CFGs, and empty
intersection of CFGs.
- Rice's theorem.
Important topics to be treated later on:
Monday, May 13 & Wednesday, May 15
I introduced, for every function f(n) on the length n of the input
string, the complexity classes TIME(f(n)), NTIME(f(n)), SPACE(f(n))
and NSPACE(f(n)). These give worst case upperbounds for the time
(measured in steps) and the space (measured in tape cells) it takes
to solve a problem on a deterministic, respectively nondeterministic,
Turing machine. I also discussed the relations between these classes,
and defined the classes P, NP, PSPACE and NPSPACE. Details are in the
handout complexity classes.
Monday, May 20
Giving an example of a polynomial-time algorithm, I showed that the
problem PATH is in P (even though the most simpleminded
algorithm is not in P).
I explained that the class NP can be seen as the class of problems
with polynomial time verifiers, and showed that the problem
CLIQUE is in NP. Other examples of problems in NP can (and
should) be found in the book.
It is a famous open problem whether P = NP. Most computer scientists
think this is not the case.
I introduced the concept of a polynomial time reduction.
Then I explained the notion of NP-completeness and mentioned that
SAT and even 3SAT is an NP-complete problem (the first
one ever found, by Cook). Using this, I showed that also CLIQUE
is NP-complete, by providing a polynomial time reduction from
3SAT to CLIQUE.
In the book there are many more NP-complete problems, which are
assigned reading (although you do not have to know hard proofs like the
NP-completeness of HAMILTONIAN PATH). Showing NP-completeness
is a skill that is a vital part of this course, and you should
practice on your own to get the necessary experience.
Wednesday, May 22
I showed that the class of context-free languages is included in P
(Sipser Thm. 7.14).
Then I proved Savitch's theorem, saying that
if f(n) 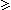 log(n) then NSPACE(f(n))
log(n) then NSPACE(f(n))
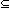 SPACE(f(n)2).
I also recalled that if a language is in NTIME(f(n)), then there is a
constant d such that it is in TIME(df(n)).
Thus, whereas converting nondeterministic machines into deterministic
ones costs us an exponential in time, it costs only a square in space.
It follows that the classes PSPACE and NPSPACE coincide.
SPACE(f(n)2).
I also recalled that if a language is in NTIME(f(n)), then there is a
constant d such that it is in TIME(df(n)).
Thus, whereas converting nondeterministic machines into deterministic
ones costs us an exponential in time, it costs only a square in space.
It follows that the classes PSPACE and NPSPACE coincide.
I discussed the hierarchy of complexity classes
L 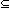 NL
NL 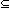 P
P 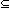 NP
NP 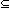 PSPACE = NPSPACE
PSPACE = NPSPACE 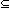 EXPTIME
EXPTIME 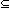 EXPSPACE.
EXPSPACE.
The concept of a polynomial-time reduction can also be used to define
PSPACE-completeness, EXPSPACE-completeness, etc., and likewise
NP-hardness, PSPACE-hardness, etc. (A problem is X-complete iff it is
X-hard and in class X.)
Friday, May 25
Arun gave today's section.
Here is his handout.
Monday, May 27 is labor day: no class
Wednesday, May 29
I showed why SAT and 3SAT are NP-complete.
Then I presented the TQBF (truth of quantified
boolean formulas) problem, which is complete for PSPACE.
I also showed how the generalized geography game can be proven
PSPACE-complete by means of a polynomial time reduction from
TQBF. Then I introduced log-space reductions, and told that the
PATH problem is NL-complete.
Friday, May 31
Elena gave today's section.
Here are her notes.
Monday, June 3
Today I showed the NL-completeness of PATH.
Subsequently I reviewed the hierarchy of complexity classes.
That NL 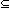 P follows because
PATH is in P, and is NL-complete, and any log-space reduction
is a polynomial time reduction.
P follows because
PATH is in P, and is NL-complete, and any log-space reduction
is a polynomial time reduction.
For any class X there is a class co-X of complements of problems in X.
When X is defined in terms of deterministic Turing machines, trivially
co-X = X. It is an open problem whether NP = co-NP.
Surprisingly, co-NL = NL. This follows because PATH is in NL
(the proof of which has been skipped).
Subsequently I presented, without proof, the time and space hierarchy
theorems that say that for time constructible functions such that one
is larger than the other by more than a logarithm, the corresponding
time complexity classes are different. Likewise, for space
constructible functions such that one is larger than the other by more
than a constant factor, the corresponding space complexity classes are
different.
Finally, I argued that through a suitable encoding of natural numbers as
strings, the concepts of decidability and enumerability apply not only
to languages, but also to sets of natural numbers. It doesn't matter which
encoding is chosen, because there must be an algorithm to convert one
encoding into an other. When the encodings are reasonable, such as the
standard n-ary or n-adic representation
of numbers as strings, one encoding can be retrieved from another
in polynomial time (or better), so even most complexity classes are
well-defined for sets of natural numbers.
I explained that the n-adic representations
yields a bijective correspondence between strings over an n-letter
alphabet and natural numbers, and pointed out the difference between
n-ary and n-adic representations.
Covered material on complexity theory: Sipser Chapters 7
(except for Theorem 7.13 and the proof of Theorem 7.35), 8 (except for
the proofs of Theorem 8.8 and 8.22 (so the statements of these
theorems are covered)) and 9.1 (except for the proofs of Theorems 9.3,
9.10, and 9.15), as well as the handout
on complexity classes.
This corresponds to HMU Chapters 10 and 11.1-3, plus the handout.
The material on the classes L and NL is not in HMU; students who are
not in the possession of Sipser should collect a copy of those parts.
Important topics:
- The complexity classes TIME(f(n)), NTIME(f(n)), SPACE(f(n)) and
NSPACE(f(n)), and their relationships.
- The classes L, NL, coNL, P, NP, coNP, PSPACE, NPSPACE, EXPTIME
and EXPSPACE and their relationships.
- The relationship between the classes of regular, context-free,
and context-sensitive languages and the classes above.
- Polynomial time reductions and the notions of
NP-completeness, PSPACE-completeness and EXPSPACE-completeness.
- Log-space reductions and the notion of NL-completeness.
- The problems SAT, 3SAT, Clique, directed and undirected
Hamiltonian path, subset-sum, and node-cover (or vertex-cover) are
NP-complete; PATH is NL-complete and in P. TQBF (even in prenex
conjunctive normal form) and the geography game are PSPACE-complete.
- The time and space hierarchy theorems.
Wednesday, June 5
Today I introduced a class of languages that is even larger than the
recursive enumerable languages, and includes all languages that have
been mentioned as examples or counterexamples at any time in this
course so far. I would have liked to introduce a class of definable
languages, such that any language that can be described in words is
definable. The Post Correspondence Problem (and language) for instance
is not recursive enumerable, but surely definable, because the
definition is in the book. In fact it is impossible to mention an
example of an undefinable language, as any way of mentioning it
involves or constitutes a definition. Nevertheless, as definitions can
be put into words, there can only be countably many definable
languages, whereas the set of all languages is uncountable. Thus most
languages are not definable, even if we cannot point at any example.
Sadly, the above plan is bogus, because
the concept of definability is ill-defined. The best one can do is
to define particular tools for defining languages, and consider classes
of languages that are definable with those tools. An extremely fruitful
tool is first-order arithmetic. One defines the arithmetical
languages as those that can be defined by arithmetical means.
This turns out to be a very large class that surely contains every
language that has been contemplated in this course so far.
I proved that the class of arithmetical languages at least contains
all recursive enumerable languages, by showing that the behavior of
any Turing machine can be encoded in terms of first-order arithmetic.
This also yielded the undecidability
of arithmetic, and Goedel's incompleteness theorem.
Thursday, June 6
There was a final exam review session, presented by Aaron, on
Thursday morning from 10:00 to 10:50am in McCullough 115, live on
channel E4. Do read his notes with tips on how to prepare for the exam:
page 1,
page 2,
page 3,
page 4,
page 5 &
page 6.
Here are a few exam-level reduction
problems (also as ps and
pdf) for you to try.
 Course notes for CS154
Course notes for CS154 Course notes for CS154
Course notes for CS154 CS154N
CS154N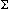 ,
and consider languages over
,
and consider languages over 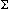 .
The acceptance problem for Turing machines, APTM is
the language
.
The acceptance problem for Turing machines, APTM is
the language
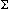 .
Because this is such an important issue I once more reviewed the
undecidability of APTM.
The language
.
Because this is such an important issue I once more reviewed the
undecidability of APTM.
The language
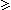 log(n) then NSPACE(f(n))
log(n) then NSPACE(f(n))
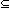 SPACE(f(n)2).
I also recalled that if a language is in NTIME(f(n)), then there is a
constant d such that it is in TIME(df(n)).
Thus, whereas converting nondeterministic machines into deterministic
ones costs us an exponential in time, it costs only a square in space.
It follows that the classes PSPACE and NPSPACE coincide.
SPACE(f(n)2).
I also recalled that if a language is in NTIME(f(n)), then there is a
constant d such that it is in TIME(df(n)).
Thus, whereas converting nondeterministic machines into deterministic
ones costs us an exponential in time, it costs only a square in space.
It follows that the classes PSPACE and NPSPACE coincide.
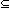 NL
NL 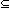 P
P 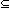 NP
NP 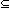 PSPACE = NPSPACE
PSPACE = NPSPACE 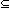 EXPTIME
EXPTIME 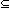 EXPSPACE.
EXPSPACE.
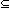 P follows because
PATH is in P, and is NL-complete, and any log-space reduction
is a polynomial time reduction.
P follows because
PATH is in P, and is NL-complete, and any log-space reduction
is a polynomial time reduction.